Reduced Order Modeling with the Mori-Zwanzig Formalism
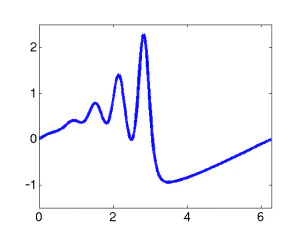 The solution to the Korteweg-de Vries equation with a smooth initial condition.
The solution to the Korteweg-de Vries equation with a smooth initial condition.
Oftentimes, when modeling natural phenomena, we have multiple choices for the scale at which we consider the problem. Consider, for example, the air molecules in the room you are in. Suppose we wish to understand how the air is moving in the room for the purposes of understanding how viral particles are distributed throughout the room from a single source. We could consider the motion of individual molecules of air and viruses. However, modeling the problem in this way is computationally intractable as one would need to keep track of trillions of variables (the location and velocity of every particle). It is also completely overkill! All the information we need can be accurately captured at a much coarser scale: the average velocity and pressure for particles at every point in the room.
Reduced order modeling is the process of taking an “overkill” model and converting it into a smaller, more tractable, “resolved” model without sacrificing any of the important features of the phenomenon we are modeling we care about. For examples like the one described above, the two scales are separated such that we can easily consider the coarser model in isolation. However, in multiscale systems, this separation is not so convenient. Consider, for example, a crack propagating through a solid. Away from the crack, molecular detail is completely overkill. Near the crack tip, however, small deviations in molecular position dictate the path of the crack as it propagates.
I use the Mori-Zwanzig formalism to convert a large system into a smaller, approximate system. The resulting approximation involves a challenging convolution integral called the “memory” term, which encodes the interactions between the variables we retain and the ones we eliminated. I developed an approach called the renormalized complete memory approximation to estimate this term.
Using Python code, I implement and perform numerical experiments using the complete memory approximation. I am most interested in applying this method to nonlinear wave partial differential equations. We have successfully applied the method to the Korteweg-de Vries equation, Burgers’ equation, and Euler’s equations in 2D and 3D.
Collaborators:
- Panos Stinis (Pacific Northwest National Laboratory)
- Brek Meuris (University of Washington)
- Madelyn Shapiro (‘20), Summer 2019
Future Projects:
- Apply the method to the nonlinear Schrodinger equation and the KdV-Burgers equation
- Improve and better understand the renormalization process
- Apply the method to other application areas