CS 361: Algorithms and Data Structures
Homework 7

Assignments will be collected at the beginning of the class period. Please bring a hardcopy to turn in. Your assignment can be hand-written or typed. Even though the book problems do not specifically say to provide a dynamic programming solution, please do so.

Written Questions

1. Algorithm Design 6.1 parts (a), (b), and (c). Note that part (c) says to "Give an algorithm". You should follow the "Homework Guidelines" when designing your algorithm. Also, your algorithm should return both the value of the independent set with maximum total weight as well as returning the independent set itself. I recommend writing two separate algorithms to do so: one to return the maximum total weight, and one to reconstruct the independent set.


2. Algorithm Design 6.2 part (b) only. Your solution should return both the value of an optimal solution as well as the solution itself. Again, I recommend that you write two separate algorithms to do so.


3. Suppose a set of n people want to organize a ski trip. They go to a ski rental shop which has m pairs of skis (where m > n). We'll let h(i) denote the height of the ith person and s(j) denote the length of the jth pair of skis.

   We want to assign each skier a pair of skis that matches their height as closely as possible. In other words, we want to assign each skier a pair of skis such that the following difference in heights is minimized:
   
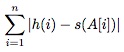
   In this equation, A[i] is the ski assignment for the ith person. For example, suppose we had the following inputs:
   
   h = [72, 73, 75] // people height in inches
   s = [63, 72, 73, 73, 77] // ski length in inches
   
   The optimal solution would be A = [2, 4, 5]. The first person is assigned the 2nd pair of skis, the second person is assigned the 4th pair of skis, and the third person is assigned the 5th pair of skis. In this case, the difference in heights is |72-72| + |73-73| + |75-77| = 2 inches.

   Design a dynamic programming algorithm that solves this problem. For this problem, you only need to return the value of an optimal solution. You are not required to return the solution itself. This problem requires you to think carefully about the various base cases that exist.