CS 361: Algorithms and Data Structures
Homework 6
Due date: 11/14 in class

This assignment has both a written and a programming portion. Both are due at the beginning of class on the 14th. The written portion will be collected at the beginning of the class period as usual. The programming portion should be uploaded to Moodle by the beginning of the class period.

For the programming, you can work by yourself or with a partner. I highly encourage you to work with a partner. If you do, be sure to put both of your names in the comment at the top of the Skiing.java file

For the questions on the written portion of the homework that ask you to "design an algorithm", your answer should include the following:

1. Description: A statement and explanation of the recursive equation you came up with that captures the structure of an optimal solution.
2. Pseudocode: Pseudocode for your algorithm. The pseudocode should give sufficient detail to make an analysis straightforward (e.g. don't hide a for-loop in an English phrase) while still being high-level enough that it can be easily read.
3. Running Time: A statement of the worst-case running time of your algorithm in Big-O notation. Please justify your running time using your pseudocode.

Written Questions

1. Given an array of positive integers A = [a₁ a₂ ... a_n] and an upper-bound W, design a dynamic programming algorithm to find a subset of A with the largest possible sum that does not exceed W. The subset does not need to be contiguous.

   For example, suppose we have an array A=[4 9 11 30 5 2] and an upper bound of W=20. Here are some possible subsets of A whose sums do not exceed 20:

   The subset {4} has a sum of 4

   The subset {9, 5} has a sum of 14

   The subset {11, 5, 2} has a sum of 18

   Your algorithm should return back the actual subset. In this case, either {9, 11} or {4, 11, 5} since both of these subsets sum to 20.

2. Design a dynamic programming algorithm to solve the problem described in Algorithm Design 6.2. For this problem, you only need to return the value of an optimal solution. You are not required to return the solution itself.

Programming Question

Suppose a set of n people want to organize a ski trip. They go to a ski rental shop which has m pairs of skis (where m > n). We'll let h(i) denote the height of the ith person and s(j) denote the length of the jth pair of skis.

We want to assign each skier a pair of skis that matches their height as closely as possible. In other words, we want to assign each skier a pair of skis such that the following difference in heights is minimized:
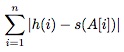
In this equation, A[i] is the ski assignment for the ith person.

This question asks you to implement a dynamic programming algorithm that solves this problem. Your program should return the actual solution in the form of an array of length n where the ith entry is the ski assignment for person i. For example, suppose we had the following inputs:

h = [72, 73, 75] // people height in inches
s = [63, 72, 73, 73, 77] // ski length in inches

The optimal solution would be A = [2, 4, 5]. The first person is assigned the 2nd pair of skis, the second person is assigned the 4th pair of skis, and the third person is assigned the 5th pair of skis. In this case, the difference in heights is |72-72| + |73-73| + |75-77| = 2 inches. Please return your solution in base-1 indexing since this is easier to read than base-0.

I have provided you with starter code for this question in the form of a Java file named Skiing.java. Inside, I have provided code for randomly generating arrays of human heights and ski lengths. I tried to generate realistic lengths so you'll notice both human and ski heights range between 61 inches (5 feet 1 inch) and 77 inches (6 feet 5 inches).

You are free to add whatever static methods and variables you'd like however you should make sure that your final solution is implemented in the computeSolution() method. The input to this method will be an array of length n. The computeSolution() method should fill this array with the optimal assignment of skis to skiers. Just like we've done in class, it's a good idea to write one method that computes the value of the optimal solution and another method that uses this to compute the actual solution.

Submission Instructions