1. (20 pts.) What is a formal system? What are the parts of a formal system?
2. Give brief definitions of the following terms (5 pts. each)
a. Interpretation
b. Model
c. Categorical (as in "The set of axioms for hyperbolic geometry is categorical"
d. Isomorphism
(problem 2, continued)
e. Sufficient condition
f. Contrapositive
g. Inversion
h. Angle of parallelism
3. (10 pts.) What are the axioms for a projective plane? Describe (very briefly) a model for a projective plane?
4. (10 pts.) Define "equivalence relation" and demonstrate (very informally) that the relation of being parallel in Euclidean geometry is an equivalence relation. Where is Euclid's postulate needed?
5. (20 pts.) On page 226, our author makes the following statement: "Had Saccheri, Legendre, F. Bolyai, or any of the dozens of other scholars succeeded in proving Euclid V from the other axioms, with the noble intention of making Euclidean geometry more secure and elegant, they would have instead completely destroyed Euclidean geometry as a consistent body of thought!" What does he mean?
6. Some basic hyperbolic stuff (10 pts. each)
a. Demonstrate that if P*A*B*C*Q in the Poincaré model with P and Q ideal points and A, B, and C ordinary points, then
P(AC) = P(AB) + P(BC)
Where P is the Poincaré distance. A formal proof is not necessary here - a calculation is sufficient.
b. Give an example of two asymptotically parallel lines in
i. The Klein model
ii. The Poincaré model
c. Given the two parallel lines in the Klein model as below: Sketch the common perpendicular. Include all work (no credit can be given for the common perpendicular without a sketch of the justification for it)
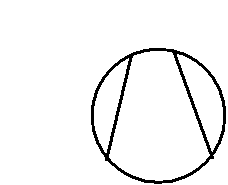
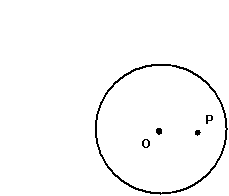
d. In the following picture, sketch the inverse of the point P (once again, including the details of your construction).
7. (20 pts.) Prove that if P and Q lie on a circle, then the center of the circle lies on the perpendicular bisector of the segment PQ.
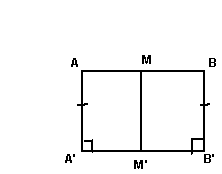
8. (20 pts.) Given a Saccheri quadrilateral AA'B'B with base angles AA'B' and BB'A' right angles and AA' congruent to BB', let M be the midpoint of the segment AB and M' be the midpoint of the segment A'B'. Show that MM' is perpendicular to AB. (Five points extra credit - show that it is also perpendicular to A'B'). What is the role of this fact in hyperbolic geometry?
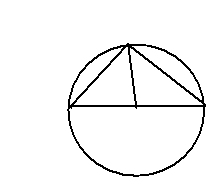
9. (20 pts.) Assuming the parallel postulate, demonstrate that a triangle inscribed in a semicircle is a right triangle (Hint: draw a radius between the center of the circle and the vertex of the angle we want to prove is a right angle, and use a fact about the sum of the angles of a triangle if the parallel postulate is true).
5. (10 pts. extra credit) When Reuben Hersh describes a working mathematician as a "Platonist on the weekdays" and a "formalist on Sundays", what is he talking about?